#1 : géométrie | #2 : arithmétique | #3 : déchiffrement | #4 : probabilités | #5 : logique | #6 : orthographe | #7 : labyrinthe | #8 : calcul matriciel | #9 : gogolplex
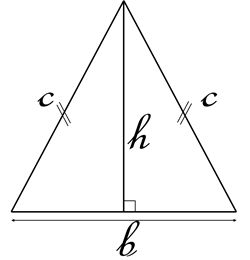Considérons un triangle isocèle de base b, de côtés c, et de hauteur h et pour lesquels b, c et h sont des nombres entiers.
Les grecs savaient déjà qu'aucun triangle ne vérifie b=h, quand b, c et h sont entiers.
Intéressons-nous à la famille de triangles pour lesquels b et h sont proches, plus précisément pour lesquels b= h ±1.
Les deux plus petits triangles répondant à ces critères sont :
- c=17, b=16 et h=15
- c=305, b=272 et h=273
Petite vérification pythagoricienne pour le premier : (b/2)²+h² = (16/2)²+15²=64+225=289=17²=c² ■
Pour résoudre cette énigme, il vous faudra trouver les 50 premiers triangles de cette famille.
Notons c(n) la longueur du côté du n-ième triangle et m(n) le chiffre du milieu de c(n). Par exemple, c(1)=17 et m(1) n’est pas défini ; c(2)=305 et donc m(2)=0.
Les coordonnées de la cache sont :
- N48°AB.CDE où A=m(21) ; B=m(24) ; C=m(50) ; D=m(21) ; E=m(15)
- E002°FG.HIJ où F=m(13) ; G=m(40) ; H=m(50) ; I=m(23) ; J=m(7)
La cache est un cryptex :
Vous obtiendrez le code d’ouverture de la cache avec le geochecker (ce n'est pas la peine d'aller sur place s'il n'est pas vert) :
FTF : stroumpf