Když se rekne krychle, tak je každému jasné, o co jde.
Klasická krychle má 3 rozmery. Ale jak by vypadala krychle, která
má 2 rozmery? Ano, jednalo by se o ctverec. Analogicky bychom
došli k záveru, že 1-rozmerná krychle je úsecka a
0-rozmerná krychle je bod. Každou krychli až do tretího
rozmeru si dokáže každý jiste nakreslit na kus papíru. A
z obrázku pak vycíst, kolik má každá n-rozmerná krychle rohu,
kolik má hran a kolik ploch.
Do ted to bylo jednoduché! Ale co když se vydáme opacným
smerem a vydáme se do N>3? Jak by na papíre vypadala 4-rozmerná
krychle? Pro ukázku jsem vám ji tady zobrazil.
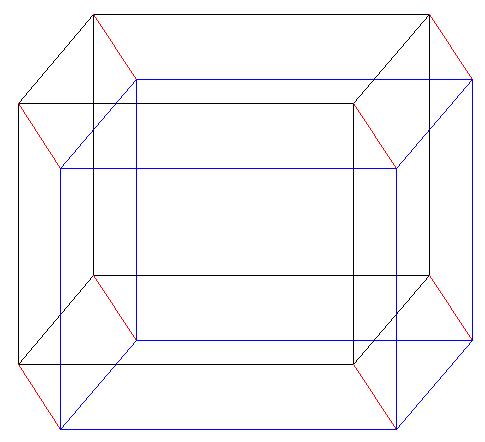
Nakreslete klasickou 3-rozmernou krychli a pak z každého
rohu vyneste stejne dlouhou úsecku pod stejným úhlem. Když
všechny koncové body spojíte, vytvorili jste 4-rozmernou
krychli. Pocet rohu si zde urcite hrave spocítáte. Spocítat hrany
už bude složitejší. Ale jak na pocet ploch? Pro
lepší orientaci zde uvádím tabulku:
| Rozmer |
Rohy |
Hrany |
Plochy |
| 0 |
1 |
0 |
0 |
| 1 |
2 |
1 |
0 |
| 2 |
4 |
4 |
1 |
| 3 |
8 |
12 |
6 |
| 4 |
16 |
? |
? |
| 5 |
? |
? |
? |
| 6 |
? |
? |
? |
| 7 |
? |
? |
? |
| 8 |
? |
? |
? |
| 9 |
? |
? |
? |
| 10 |
1024 |
5120 |
11520 |
| 11 |
? |
? |
? |
| 12 |
? |
? |
? |
| 13 |
? |
? |
? |
| 14 |
? |
? |
? |
| 15 |
? |
? |
? |
Takhle bysme mohli pokracovat až do nekonecna. Urcite se
shodneme na tom, že je cirý nesmysl si kreslit na papír napr.
6-rozmernou krychli a všechno u ní vizuelne pocítat.
Nejjednoduší bude si vytvorit vzorecek, který pak
mužeme aplikovat na každý rozmer. Ale to už nechám
na vás. Pro zjednušení oznacme pocet rohu písmenem R, pocet
hran písmenem H a pocet ploch písmenem P. Císlo v závorce bude
udávat daný rozmer. Finálku najdete na souradnicích:
50°10.H(7)+P(6)-R(5)-R(0)+75
014°30.P(8)-H(8)-R(8)-H(6)-R(6)+R(1)+P(2)+736
Finální souradnice se dne 29.1.2011 zmenily!!!
