Een lid van het team is laatst afgestudeerd aan de TU Delft. Om dat te vieren hebben we deze cache geplaatst. De puzzel bestaat uit een aantal stappen die in het eerste jaar van de opleiding Luchtvaart- en Ruimtevaarttechniek behandeld worden. Als je alle stappen volgt kun je de vraag zo oplossen.
De vraag:
Voor twee verschillende vliegtuigen willen we weten wat de afstand is tussen het opstarten en loskomen van de grond bij het opstijgen. Het antwoord voor vliegtuig 1 is ABCD, voor vliegtuig 2 EFGH. De cache ligt op
N 51° 5A.BCD E 004° 2E.FGH
Om dit uit te rekenen heb je de volgende informatie nodig*:
*getallen komen niet met de werkelijkheid overeen: ze zijn alleen gekozen omdat ze mooi uitkomen met de cachelocatie. In het echt zou je dit soort waardes ook nooit zo nauwkeurig weten, maar ook dat is omdat anders het resultaat niet samenvalt met de cachelocatie.
| |
symbool |
Vliegtuig 1 |
Vliegtuig 2 |
| Gewicht \([kg]\) |
m |
15999.3 |
16641.09 |
| Vleugeloppervlakte \([m^2]\) |
A |
100.729 |
120.548 |
| Voortstuwingskracht \([kN]\) |
T |
35.9849 |
33.239 |
| Liftcoëfficient \([-]\) |
\(C_L\) |
1.38023 |
1.557 |
| Luchtweerstandscoëfficiënt \([-]\) |
\(C_D\) |
0.314992 |
0.21946 |
| Rolcoëfficient voorste wiel \([-]\) |
\(\mu_1\) |
0.10087 |
0.1013 |
| Rolcoëfficient achterste wielen \([-]\) |
\(\mu_2\) |
0.203966 |
0.2056 |
| Afstand tussen voorste wiel en zwaartepunt \([m]\) |
\(L_1\) |
13.295 |
13.394 |
| Afstand tussen voorste wiel en achterste wielen \([m]\) |
\(L_2\) |
14.929 |
14.964 |
| Valversnelling \([m/s^2]\) |
g |
9.81 |
9.81 |
| Luchtdichtheid \([kg/m^3]\) |
\(\rho\) |
1.225 |
1.225 |
Ook mag je aannemen dat:
- De gewichtsafname door brandstofgebruik verwaarloosbaar is
- De geleverde kracht door de motoren constant is
- Het vliegtuig opstijgt op het moment dat de lift \(\ge\) de zwaartekracht
- Het windstil is
- De center of lift en het zwaartepunt samenvallen (dit is in het echt niet zo, voor meer informatie, zie hier)
- De krachten in het horizontale vlak (wrijving van de wielen/vleugels en de kracht van de motoren) in lijn liggen met zwaartepunt (en dus niet mee hoeven te worden genomen in de som van de momenten)
Stap 1:
Als eerste moeten we uit kunnen rekenen wat de krachten op het vliegtuig zijn. In dit geval zijn het er 6:
- De zwaartekracht: \(F_z = m \cdot g\)
- De lift, gegenereerd door de vleugels: \(L = \frac{1}{2}\cdot \rho \cdot V^2\cdot A\cdot C_L\)
- De wrijvingskracht, ook gegenereerd door de vleugels: \(D = \frac{1}{2}\cdot \rho \cdot V^2\cdot A\cdot C_D\)
- De voortstuwingskracht \(T\), gegenereerd door de motoren (let erop, deze is gegeven in \([kN]\), en \(1 kN = 1000 N\)!)
- De normaalkracht, geleverd door de wielen: \(F_n\), op dit moment onbekend
- De rolweerstand geleverd door de wielen: \(F_w = F_n \cdot \mu\)

Van de bovenstaande formules zijn die voor de lift en voor de wrijvingskracht het minst bekend. Deze formules lijken erg op elkaar, en bestaan uit drie delen:
- Een dynamische druk \(\frac{1}{2}\cdot \rho \cdot V^2\), met \(\rho\) als de luchtdichtheid in \([kg/m^3]\)en \(V\) als de snelheid van het vliegtuig ten opzichte van de lucht in \([m/s]\)
- Het vleugeloppervlak \(A\) in \([m^2]\)
- Een coëfficient afhankelijk van de vleugelvorm.
Dus eigenlijk staat hier:
- voor de lift: als je harder vliegt, met grotere vleugels, en een betere vorm (hogere \(C_L \)), dan ga je meer omhoog.
- voor de wrijvingskracht: als je harder vliegt, met grotere vleugels, en een slechtere vorm (hogere \(C_D\)), dan krijg je meer wrijvingskracht.
Als je meer wilt weten over liftcoefficiënten, klik dan hier. Voor meer informatie over wrijvingscoëfficienten, klik dan hier en hier
Stap 2:
Om uit te rekenen wat de normaalkracht is op elk van de wielen kunnen we gebruik maken van de theorie die bekend staat als statica. Hierbij zijn twee formules van belang:
- Som van de krachten is nul: \(\Sigma F = 0\)
- Som van de momenten is nul: \(\Sigma M = 0\)
De som van de krachten in de x-as zijn natuurlijk niet 0, anders zou er geen versnelling zijn bij het opstijgen. In de z-as is dit wel het geval zolang het vliegtuig contact maakt met de grond.
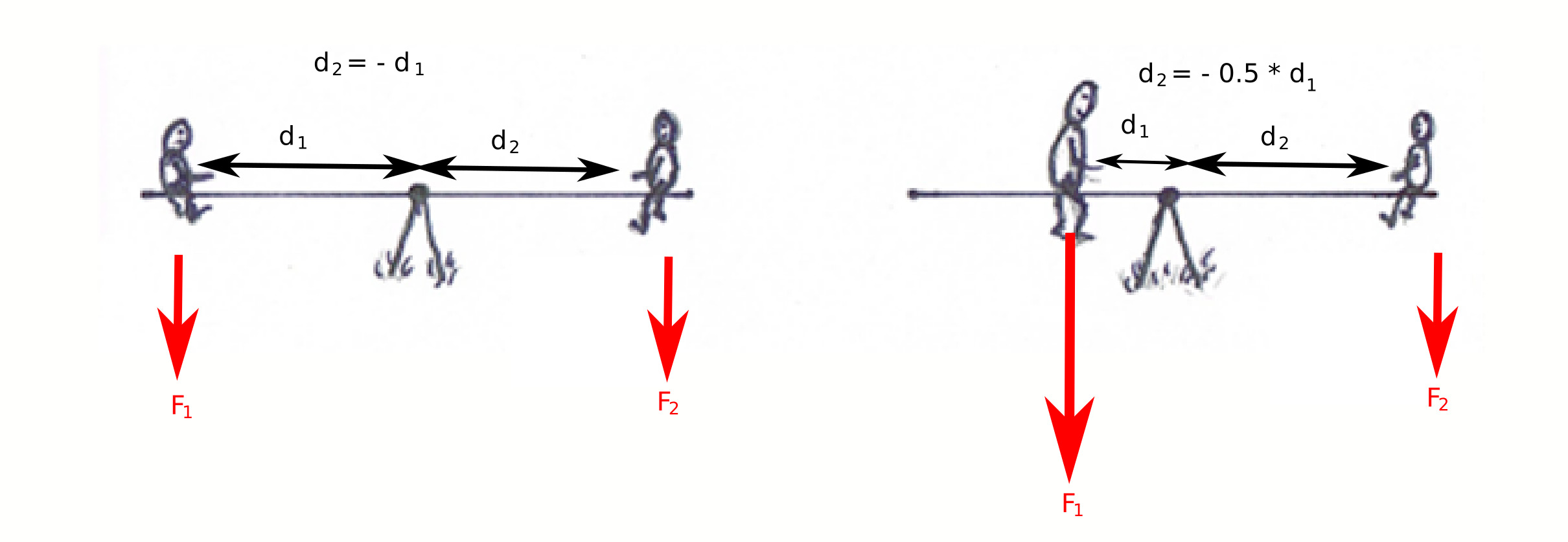
Een logische vraag om nu te stellen is, wat betekenen deze formules? De som van de krachten zal misschien wel bekend zijn, maar som van de momenten is toch al wat obscuurder. Om dit uit te leggen gebruiken we het voorbeeld van de wipwap:
Als je op een wipwap zit en je bent precies even zwaar en zit even ver van het midden af, dan kun je zonder veel moeite op en neer bewegen: je bent namelijk in evenwicht.
Maar als de ene persoon twee keer zoveel weegt als de andere, dan is er een probleem: de lichtste bungelt maar in de lucht! Dit kun je oplossen als de zwaarste persoon dichter bij het midden gaat zitten. Als de afstand tot het midden x het gewicht van de persoon gelijk is voor allebei de kanten, dan is de som van de momenten nul.
In formules geschreven: \(\Sigma M = F_1 \cdot d_1 + F_2 \cdot d_2 .... = 0\) Houdt hiermee rekening dat de arm ook een negatieve waarde kan hebben, zoals in de tekening hieronder.
Hiermee kun je uitrekenen wat de krachten op de wielen zijn. Zie de schets hier beneden. Om te zorgen dat het vliegtuig in evenwicht is, moet de som van de moment nul zijn en de som van de krachten nul. In dit geval is de kracht op het achterste wiel:\(F_{n2 } = \frac{F_z \cdot L_1 - L\cdot L_1}{L_2}\)
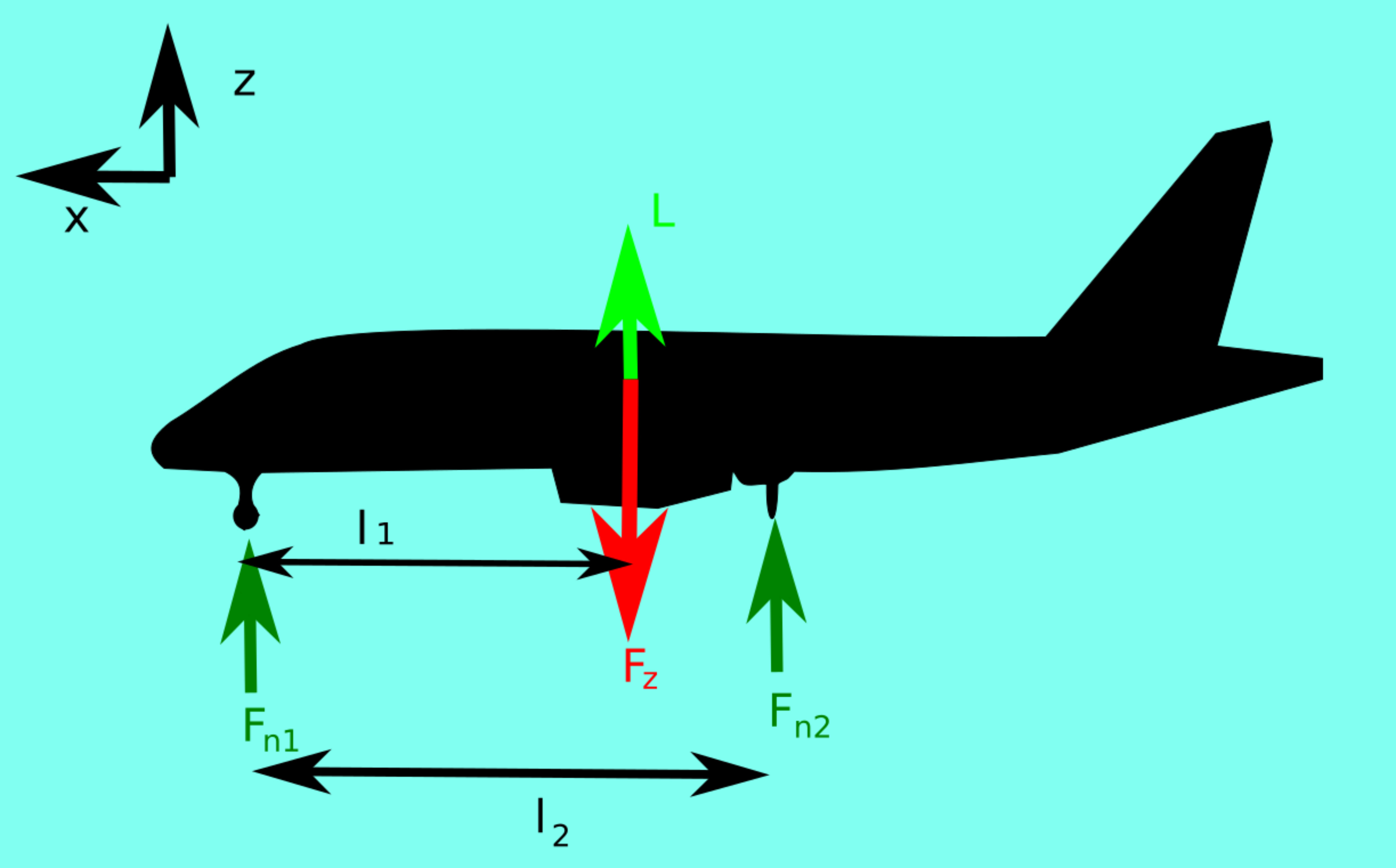
\(\)De totale kracht in de z-richting moet ook nul zijn, anders zou het vliegtuig door de grond zakken of al opstijgen. Dit betekent dat \(F_{n1} = F_z - L - F_{n2}\)
Nu kunnen we ook de rolweerstand van de voorste en achterste wielen uitrekenen: \(F_w = F_n \cdot \mu\). De rolweerstand is de normaalkracht keer de rolcoëfficient.
Stap 3:
Nu kunnen we uitrekenen hoe snel het vliegtuig versnelt. Dit doen we met de formule \(F = m\cdot a\). Hierbij is \(F = T - D - F_{w1} - F_{w2}\) de kracht van de motoren min de wrijvingskracht en rolweerstand. \(m\) Is het gewicht van het vliegtuig in \([kg]\). Op deze manier kunnen we voor elk willekeurig moment uitrekenen wat de versnelling is van het vliegtuig.
Stap 4:
Nu is de vraag natuurlijk hoe we al deze informatie gaan gebruiken. Eerst vatten we samen wat we tot nu toe gedaan hebben:
- Als we de snelheid weten, kunnen we de lift en wrijving uitrekenen
- Met de lift en het gewicht kunnen we de kracht op de wielen uitrekenen
- Hiermee rekenen we de rolweerstand uit
- Daarmee kunnen we uitrekenen hoe hard we versnellen
Nu willen we dit allemaal samen brengen in 1 berekening om erachter te komen hoe ver de vliegtuigen rijden voordat ze op kunnen stijgen. Dit doen we met python, een programmeertaal (je mag ook excel gebruiken), hier kun je met python een scriptje schrijven.
Hoe werkt dit?
Eerst schrijven we op wat de beginwaardes zijn:
x = 0 #m (we staan nog op het startpunt)
v = 0 # m/s
m = 100 # kg
g = 9.81 # m/s^2
luchtdichtheid = 1.225 # kg/m^3
A = 100 # m^2
c_L = 1 # -
c_d = 0.2 # -
mu_voor = 0.15 # -
mu_achter = 0.07 # -
lengte_1 = 20 # m
lengte_2 = 15 # m
thrust = 10 # kN
Wat staat hier? Elke regel bestaat uit 3 onderdelen:
de_naam = waarde # uitleg
de_naam en waarde is wat de computer gebruikt, je kan bijvoorbeeld schrijven:
a = 5
b = 4
c = a + b
print(c)
Als je dan op het "run" knopje drukt krijg je terug:
9
Alles wat achter het # staat slaat de computer over. Dat is alleen voor jezelf om het makkelijk te maken.
We kunnen nu ook formules gebruiken om uit te rekenen hoe snel het vliegtuig versnelt:
# reken uit wat de zwaartekracht is:
F_z = m * g
# reken uit wat de lift is:
L = 0.5 * luchtdichtheid * V * V * A * c_L
# reken uit wat de normaal kracht is op het voorste wiel
F_n1 = (lengte_1 * F_z - lengte_1 * L) / (lengte_2)
# reken uit wat de kracht is op het achterste wiel
F_n2 =
# reken uit wat de rolweerstand is van het voorste wiel
F_w1 =
# reken uit wat de rolweerstand is van de achterste wielen
F_w2 =
# reken uit wat de totale voowaartse kracht is:
F =
# reken uit wat de versnelling is
a = F / m
Hiermee kunnen we uitrekenen hoe hard het vliegtuig over bijvoorbeeld 1 seconde ongeveer zal gaan en hoe ver het heeft gereden:
dt = 1 #seconde
x += v * dt
v = v + a * dt
we hebben nu een nieuwe positie en een nieuwe snelheid, en kunnen deze stappen herhalen totdat we opstijgen! Dit kan heel handig met een while loop. Hiermee kun je iets telkens opnieuw doen, totdat er "iets" gebeurt. Bijvoorbeeld:
a = 1
while a < 10:
# dit betekent: a = a + 1, oftewel, a wordt 1 groter
a += 1
print('a is', a)
Dit kunnen we gebruiken om uit te rekenen hoelang het duurt voordat we opstijgen:
F_z = m * g
dt = 1
# hier staat: terwijl de zwaartekracht (m * g) groter is dan de lift kracht, doe dan
while F_z > 0.5 * luchtdichtheid * V * V * A * c_L:
# reken alle krachten en versnellingen uit
x += v * dt
v += a * dt
Dit process noemen we "numerieke tijdsintegratie", een heel nuttige manier om dingen uit te rekenen die met de hand vaak veel te moeilijk zijn.
Het is natuurlijk logisch dat deze berekening nauwkeuriger wordt als je de tijdstapjes kleiner maakt. Als je de tijdstappen heel groot maakt, bijvoorbeeld 100s, dan lijkt het namelijk alsof we na 100 seconden nog geen een meter zijn opgeschoten! Met heel kleine tijdsstapjes (0.00000001 seconde) krijg je een heel nauwkeurig antwoord, maar dit duurt heel lang om uit te rekenen. Om erachter te komen of je tijdstap klein genoeg is kun je een aantal experimenten doen. Reken eerst met een tijdstap van 1 seconde, dan 0.1 seconde, dan 0.01 seconde. Op een gegeven moment verandert het antwoord nauwelijks meer en weet je dat je goed zit.
Er zijn ook manieren om met grotere tijdstappen toch nauwkeurige antwoorden te krijgen. Er is hier heel veel knappe wiskunde over bedacht (zie bijvoorbeeld: de runga-kuttamethode), maar dat is in dit geval niet nodig. De die hard wiskundigen onder ons mogen ook proberen dit probleem met een differentiaal vergelijking op te lossen
Met dank aan de zoon van a.vandiepen voor de verbeterpuntjes!