Mens Agitat Molem

Aan de oever van de Dommel

Ter gelegenheid van het 50 jarig bestaan van de Technische Universiteit Eindhoven, kortweg TU/e hebben twee oud wiskunde-studenten hier hun eerste geocache geplaatst op de campus. Om de geocache te vinden is enige middelbare school wiskunde kennis nodig. Aangezien deze kennis misschien wat is weggezakt zijn in de tekst wiskundige anekdotes en uitleg opgenomen. De tekst in de kaders is puur ter leering ende vermaeck, dus niet nodig om de cache te vinden.

Het TU/e terrein is toegangelijk tussen zonsopkomst en zonsondergang.

Waypoint 0: N 51º 27.143, E 5º 29.457

Hier kunt u eventueel (gratis) parkeren op de ventweg.

Puzzel: Los op

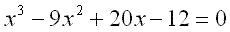
Noem de wortels van deze vergelijking A, B, en C, waarbij A < B < C.

Waypoint 1: N 51º 27.0BC, E 5º 29.BAA

Opdracht: Tel het aantal ronde buizen (horizontaal en verticaal) van het groene hek, en tel hier 2 bij op. Dit getal is s.
Puzzel: Bepaal het 7e getal in de Fibonacci-reeks 5, 4, 9, 13, … en vermenigvuldig dit getal met s. Noteer de uitkomst als FGH.

Leonhard Euler (1707 - 1783, Zwitserland) Euler loste het wiskundig vraagstuk 'de zeven bruggen van Königsberg' op. In de geschiedenis van de wiskunde is het één van de eerste grafentheoretische problemen. De stad Königsberg lag aan de rivier de Pregel, waarin twee eilanden lagen die door zeven bruggen met elkaar en met de vaste wal verbonden waren. De vraag was nu of het mogelijk is om zó te wandelen dat je precies één maal over elke brug liep en weer op het startpunt eindigde. In 1736 heeft Euler aangetoond dat dit onmogelijk is. Tevens heeft hij laten zien dat het probleem beschouwd kan worden als een probleem op een graaf, waarin de bruggen van Königsberg als volgt gemodelleerd zijn: 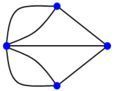Euler toonde aan dat zo'n wandeling dan en slechts dan mogelijk is als er geen punten zijn (met blauw aangegeven in de afbeelding) die grenzen aan een oneven aantal lijnen. Zo'n wandeling heet een Eulertoer. Omdat de graaf van Königsberg vier punten heeft die aan een oneven aantal lijnen grenzen, is de wandeling onmogelijk. Als het startpunt niet gelijk hoeft te zijn aan het eindpunt, kunnen er hoogstens twee punten zijn die aan een oneven aantal lijnen grenzen. Zo'n wandeling wordt een Eulerwandeling genoemd. In een knoop met een oneven aantal aansluitende lijnen, móet de wandeling ófwel starten ófwel stoppen; wanneer de knoop gewoon gepasseerd wordt kunnen immers twee wegen niet meer gebruikt worden. Op het einde blijft dan één weg achter, die enkel gebruikt kan worden als in de knoop gestopt wordt.

Waypoint 2: N 51º 26.FGH, E 5º 28.HCC

Opdracht: Tel het aantal letters van het eerste + het laatste woord van het parool van de TU/e, en noem dit aantal n.
Puzzel: Bepaal de coordinaat (J,K) van het (locale) maximum van de functie

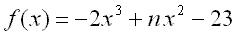
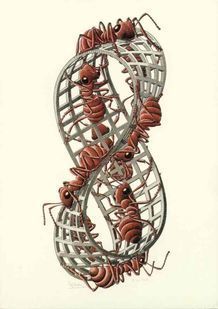
Augustus Ferdinand Möbius (1790 - 1868, Duitsland) Hij is vooral bekend van zijn ontdekking van de Möbiusband, een tweedimensionaal oppervlak met slechts één kant indien ingebed in driedimensionele Euclidische ruimte. De Möbiusband of band van Möbius is een bijzondere ruimtefiguur, genoemd naar de ontdekker ervan, August Ferdinand Möbius. De band bestaat namelijk alleen uit een plat vlak, maar kan alleen in de driedimensionale ruimte bestaan. Beroemd is de weergave van Escher, die de Möbiusband wel driedimensionaal afbeeldt, namelijk als een rooster, waarop mieren lopen. De eigenschappen van de band van Möbius zijn namelijk zodanig, dat deze ruimtefiguur slechts 1 kant en 1 rand heeft. Volgt men de mieren op hun tocht, dan zal blijken dat ze oneindig door kunnen lopen zonder een rand om te gaan, en toch het hele oppervlak bewandelen. Het is eenvoudig om zelf een Möbiusband te maken: neem een strook papier, breng de uiteinden bij elkaar en draai een van de uiteinden een halve slag. Plak de einden vervolgens op elkaar. Klaar om te experimenteren!

Waypoint 3: N 51º 26.GBJ, E 5º 29.KJJ

Opdracht: Bepaal de som der cijfers van het telefoonnummer (incl. netnummer) op het Meetpunt Kathodische Bescherming. Noem deze som s.
Puzzel: Bereken s - GGD(120, 136). Noteer de uitkomst als LM.

Euclides (3e eeuw voor Chr, Griekenland) Het algoritme van Euclides, genoemd naar de Griekse wiskundige Euclides, is een algoritme voor het bepalen van de grootste gemene deler van twee gehele getallen. Noem het grootste van de beide getallen A, het andere B. Trek B net zo vaak van A af totdat er 0 over blijft of een getal kleiner dan B. Wanneer er 0 over blijft zijn we klaar, en is B de ggd. Zo niet, herhaal dan het algoritme met B en wat er van A over is. De grootste gemene deler, afgekort met GGD van een aantal gegeven getallen is het grootste getal waar alle gegeven getallen door gedeeld kunnen worden. Bijvoorbeeld de grootste gemene deler van 6 en 12 is het getal 6. De grootste gemene deler van 15 en 20 is het getal 5. Bij het vereenvoudigen van een breuk is het handig om de GGD te bepalen. Het getal boven en onder de breuk kan dan door de GGD worden gedeeld en zo verkrijgt met direct de grootste vereenvoudiging. De breuk 24/102 wordt aldus vereenvoudigd tot 4/17. Bovenstaande voorbeelden zijn eenvoudig, maar bij grotere getallen is het niet direct duidelijk wat de GGD is. De GGD wordt bijvoorbeeld bepaald door beide getallen te ontbinden in factoren. Dat wil zeggen dat van beide getallen wordt bepaald door welke priemgetallen ze deelbaar zijn. Daarbij wordt achtereenvolgens van elk priemgetal geprobeerd of dit een deler is. Als een getal 2 of meerdere malen door hetzelfde priemgetal deelbaar is wordt dit 2 of meerdere malen genoteerd. Vervolgens worden alle gemeenschappelijk priemfactoren met elkaar vermenigvuldigd. Het resultaat is de GGD. Een voorbeeld maakt dit duidelijk: Het getal 24 is deelbaar door de priemgetallen 2, 2, 2, 3 (want 24 is gelijk aan 2 × 2 × 2 × 3) Het getal 102 is deelbaar door de priemgetallen 2, 3 en 17. De grootste gemene deler van 24 en 102 is dus 2 × 3 = 6. Een efficiënt algoritme voor het bepalen van de GGD is het algoritme van Euclides. Voor grote getallen is het algoritme van Euclides te verkiezen boven de methode met het ontbinden in factoren, omdat het ontbinden in factoren van grote getallen (zelfs voor computers) heel moeilijk kan zijn.

Waypoint 4: N 51º 27.MML, E 5º 29.GKA

Opdracht: Bepaal de kleur van de pijl op het paaltje van de “Karpen loop-/wandelroute”. Kies:

• N = 1 als de pijl wit is,
• N = 2 als de pijl groen is, en
• N = 3 als de pijl oranje is.

Pythagoras (582 voor Chr – 496 voor Chr, Griekenland) De stelling van Pythagoras is waarschijnlijk de bekendste stelling in de wiskunde. 'Zijn' stelling was overigens alleen maar nieuw voor de Grieken. In Babylonië was het resultaat al veel langer bekend. De stelling zegt iets over de relatie tussen de rechthoekszijden en de schuine zijde van alle rechthoekige driehoeken. In de rechthoekige driehoek ABC zijn de zijden a en b de rechthoekszijden. De zijde c noemen we de schuine zijde of hypothenusa. De stelling van Pythagoras luidt: "In een rechthoekige driehoek is het kwadraat van de lengte van de hypothenusa gelijk aan de som van de kwadraten van de lengtes van de rechthoekszijden." Anders geformuleerd:

Waypoint 5: N 51º 27.KNF, E 5º 30.PQM

Opdracht: bepaal de som der cijfers van het getal op het paaltje met de twee blauwe strepen. Noteer deze som als R.
Puzzel: In een geocache zitten 10 verschillende voorwerpen. Hoeveel verschillende combinaties van 2 voorwerpen kun je uit deze geocache kiezen? Noteer dit aantal als ST.

Blaise Pascal (1623 – 1662, Frankrijk) Pascal ontwikkelde de naar hem genoemde getallendriehoek naar aanleiding van het bekende problème des partis bij het dobbelen. De driehoek van Pascal is een rangschikking van de binomiaalcoëfficiënten 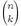(spreek uit n boven k) in rijen voor toenemende n beginnend met n=0 en op elke rij de n+1 binomiaalcoëfficiënten voor de mogelijke waarden van k. In de driehoek komt de eigenschap tot uitdrukking dat elke binomiaalcoëfficiënt de som is van de twee bovenliggende. De getallen in de driehoek geven het aantal wegen aan vanaf de top naar de plaats van zo'n getal, waarmee ook de besproken eigenschap verklaard is. Omdat er steeds 2 keuzen zijn om de weg naar onder te vervolgen is de som van de getallen op een rij de overeenkomstige macht van 2. De binomiaalcoëfficienten kunnen worden toegepast bij het tellen van combinaties. Wanneer k elementen uit een verzameling van n worden gekozen (zonder teruglegging), en waarbij de volgorde niet van belang is, dan is het aantal mogelijke manieren n boven k. Bijvoorbeeld: je hebt 8 voorwerpen, en je kiest er 3; dan zijn er 8!/3!(8 - 3)! = 56 kiesmogelijkheden.

Waypoint 6: N 51º 27.STR, E 5º 29.QFN

Opdracht: Hier staat een lantaarnpaal met daarop een 2-cijferig nummer "xy".
Puzzel: Los het volgende stelsel vergelijkingen op.

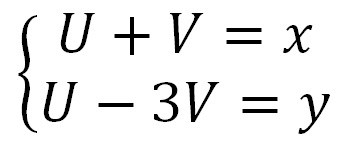
Hint: Het is vanaf hier niet meer nodig om langs de weg te lopen tot aan de cache!

René Descartes (1596 - 1650, Frankrijk) René Descartes is bekend gebleven om verschillende redenen, maar twee ontdekkingen zijn onlosmakelijk verbonden met zijn naam: naast de introductie van het cartesiaanse assenstelsel in de wiskunde, werd hij vooral bekend om zijn filosofisch werk. Zijn stelling "Ik denk, dus ik ben" (cogito ergo sum), was een poging om een filosofische bouwsteen aan te dragen voor het zijn en denken van de mens. Het oplossen van vergelijkingen is een term uit de wiskunde. Het geeft aan hoe de waarde van een onbekende, vaak aangeduid met x, kan worden bepaald uit een of meer vergelijkingen. Een vergelijking krijg je als je twee "dingen" met elkaar vergelijkt. Je wilt dan weten wat de overeenkomst is tussen die twee. Wiskundig wordt dit geschreven in formulevorm, met het teken = tussen de twee uitdrukkingen die aan elkaar gelijk zijn. In de wiskunde gebruiken we vergelijkingen bijvoorbeeld om een kromme in een tweedimensionaal coördinatensysteem vast te leggen. Elk van beide lijnen wordt dan gerepresenteerd door een betrekking tussen de coördinaten x en y. Een snijpunt van de beide krommen heeft coördinaten x en y die aan beide betrekkingen voldoen. Dat levert twee vergelijkingen met twee onbekenden x en y. Met uitzondering van evenwijdige lijnen, hebben twee rechte lijnen altijd een snijpunt. Als we het snijpunt willen weten, kunnen we de grafiek tekenen, maar dat kost erg veel tijd en veel papier als het snijpunt erg "ver" ligt! Om het snijpunt te vinden is het handiger de twee vergelijkingen op te lossen.

Waypoint 7: N 51º 27.VUS, E 5º 29.UTU

Opdracht: Welk decimaal getal bestaande uit 2 cijfers staat er op het witte plaatje op het paaltje naast een boom? Vermenigvuldig het met 60 en tel er F bij op. Noteer dit getal als WXY.
Puzzel: Bereken

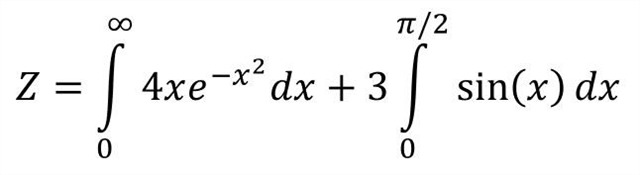
Sir Isaac Newton (1643 - 1727, Engeland) De integraalrekening werd in de 17e eeuw ongeveer tegelijkertijd met de differentiaalrekening uitgevonden door onder andere Isaac Newton. De integraalrekening is een onderdeel van de wiskunde, in het bijzonder de analyse. Men gebruikt hierin integralen voor het berekenen van totalen, zoals de totale oppervlakte onder een grafiek, de totale verandering van een gegeven grootheid als voor elk moment de verandering per tijdseenheid gegeven is of het berekenen van de massa van een voorwerp als de dichtheid op elk punt gegeven is. 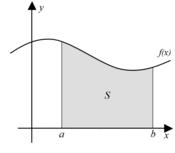In het eenvoudigste intuïtieve geval berekent men met een bepaalde integraal van een functie de oppervlakte begrensd door de functie en de coördinaatas, tussen twee punten. De integraal van een functie f over een interval [a,b] wordt geschreven als: 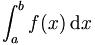Het resultaat is de oppervlakte S onder de grafiek. De integraal van f(x) is de oppervlakte tussen de curve y = f(x) en de x-as in het interval [a,b].

Waypoint 8: N 51º 27.MYM, E 5º 29.ZWS

Opdracht: Zoek de cache!

You can check your final coordinate for this geocache on GeoChecker.com.

At the bank of the Dommel

On the occasion of the 50th anniversary of the Technical University Eindhoven (TU/e) two former math students placed their first geocache on the campus of the TU/e. In order to find this geocache some elementary mathematical knowledge is required. Since your math might be a bit rusty, we added some nice mathematical anecdotes and explanation to the description above. This boxed text is for amusement only, and is not required to find the cache.

The TU/e campus is open for public between sunrise and sunset.

Beware: On August 27, 2021 the cache description has been updated and the final cache location has changed.

Waypoint 0: N 51º 27.143, E 5º 29.457

Here you can park your car (for free) at the service road.

Exercise: Solve

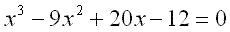
Indicate the roots of this equation by A, B, and C, such that A < B < C.

Waypoint 1: N 51º 27.0BC, E 5º 29.BAA

Assignment: Count the number of round bars (horizontally and vertically) of the green fench and add 2. This number is s.
Exercise: Calculate the 7th number of the Fibonacci-series 5, 4, 9, 13, … and multiply this number by s. Denote the result by FGH.

Leonhard Euler (1707 - 1783, Switserland) Euler solved the mathematical problem "The seven bridges of Königsberg". In the history of mathematics, this is one of the first problems in graph theory. The city Königsberg was situated at the bank of the river Pregel, in which there were two islands, that were connected to eachother and to both banks by seven bridges. The question was whether it is possible to walk around, cross each bridge exactly once, and return to the starting point. In 1736, Euler proved that this is impossible. He also showed that this problem can be seen as a graph problem, where the bridges of Königsberg are modeled as follows. Euler showed that such a tour can only exist if there are no vertices (shown in blue in the picture) that are incident to an odd number of edges. Such a tour is called an Euler-tour. Since the graph of the Königsberg problem has four vertices that are incident to an odd number of edges, no Euler-tour exists. If the start and end position do not have to be the same, then at most two vertices can be incident to an oddd number of edges. Such a walk is called an Euler-walk. An Euler-walk starts and ends in a vertex that is indicent to an odd number of edges: after all, if a vertex is passed along the walk, then two edges cannot be used anymore. In the end, only one incident edge remains, that can only be used if the walk starts or ends in that vertex.

Waypoint 2: N 51º 26.FGH, E 5º 28.HCC

Assignment: Count the number of characters of the first and last word of the TU/e slogan, and denote this number by n.
Exercise: Determine the coordinate (J,K) of the (local) maximum of the function

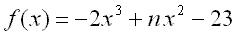
August Ferdinand Möbius (1790 - 1868, Germany) He is best known for his discovery of the Möbius-ring, a two-dimensional surface with only one side, embedded in the three-dimensional Euclidean space. The Möbius-ring is a remarkable 3D-figure, named after its discoverer, August Ferdinand Möbius. The ring consists of just a surface, but it can only exist in three-dimensional space. Escher's drawing of the Möbius-ring is well-known, it shows the ring as a lattice, with ants walking on it. The Möbius-ring has only one side, and one edge: follow the ants on their trail, and it becomes clear that the ants can walk infinitely without crossing the edge, and at the same that walk on the entire surface. It is easy to construct a Möbius-ring yourself: take a strip of paper, bring the ends (i.e. the small edges) together, and twist one of the edges half a turn. Glue the ends together. Ready to experiment!

Waypoint 3: N 51º 26.GBJ, E 5º 29.KJJ

Assignment: Determine the sum of the digits of the phone number (including the area code prefix) on the "Meetpunt Kathodische Bescherming". Denote this sum by s.
Exercise: Calculate s - GCD(120, 136). Denote the result by LM.

Euclid (3rd century BC, Greece) The algorithm of Euclid, named after the Greek mathematician Euclid, is an algorithm to determine the greatest common divisor of two numbers. Denote the largest number by A, and the other by B. Repeatedly subtract B from A, until 0 remains, or a number less than B. If 0 remains, we're done, and B is the GCD of A and B. If not, apply the same algorithm to B and what's left of A. The greatest common divisor, or GCD for short, of a set of numbers is the largest number that divides all the numbers of the set. For instance, the greatest common divisor of 6 and 12 is 6. The greatest common divisor of 15 and 20 is 5. When simplifying a fraction it is very handy to determine the GCD of the numerator and the denominator.Dividing both the numerator and the denominator by the GCD results directly in the simplified fraction. In this way, the fraction 24/102 is directly simplified to 4/17. The examples above are quite easy, but for larger numbers is it not immediately clear what the GCD is. The GCD can be determined by factoring both numbers into prime numbers. For both numbers one must determine which prime numbers divide it. If a prime divides the given number more than once, the number of possible divisions is noted. Next, all common prime numbers are multiplied, and the result is the GCD. An example will make this clear: The number 24 can be divided by the prime numbers 2, 2, 2, 3 (since 24 = 2 x 2 x 2 x 4) The number 102 can be divided by the prime numbers 2, 3, and 17. Hence, the greatest common divisor of 24 and 102 is 2 x 3 = 6. An efficient algorithm to find the GCD is the algorithm of Euclid. For larger numbers, the algorithm of Euclid is much more efficient than factoring the given numbers, since finding prime factors of large numbers is, even for computers, very difficult.

Waypoint 4: N 51º 27.MML, E 5º 29.GKA

Assignment: Determine the color of the arrow on the pole of the “Karpen loop-/wandelroute”. Choose:

• N = 1 if the arrow is white,
• N = 2 if the arrow is green, and
• N = 3 if the arrow is orange.

Pythagoras (582 b.C. – 496 b.C, Greece) The Pythagorean theorem is probably the best known mathematical theorem. Pythagoras theorem was only new for the Greeks: in Babylon this relation was already known for quite a while. The theorem defines a relation between the two rectangular edges and the third (diagonal) edge of a rectangular triangle. In a rectangular triangle ABC the edges a and b are the rectangular edges, and edge c is called the hypothenuse. The Pythagorean theorem states: in every rectangular triangle the square of the hypothenuse equals the sum of the squares of the two rectangular edges. In other words:

Waypoint 5: N 51º 27.KNF, E 5º 30.PQM

Assignment: Determine the sum of the digits on the pole with 2 blue stripes. Denote this sum by R.
Exercise: A geocache contains 10 different items. How many combinations of 2 items can you take out of this cache? Denote this number by ST.

Waypoint 6: N 51º 27.STR, E 5º 29.QFN

Assignment: Here you find a lamppost with a number "xy" of 2 digits.
Exercise: Solve the following system of linear equations.

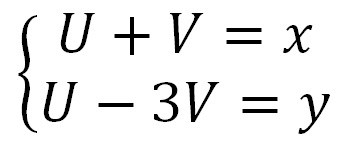
Hint: It is not necessary to walk along the main road from now until you have reached the cache!

René Descartes (1596 - 1650, France) René Descartes is well known for multiple reasons, but two discoveries are inextricably linked to him: next to the introduction of the Cartesian coordinate system in mathematics, he became also well known for his philosophical work. His statement "I think, therefore I am" (cogito ergo sum) was an attempt to define a philosophical foundation for the being and reasoning of humanity. Solving equations is a mathematical term. It tells us how the value of an unknown variable, oftern denoted by 'x', can be derived from one or more equations. An equation is obtained by comparing two "things" with eachother. You want to known what the relation is between these two items. In mathematics this is denoted in a formula, using the sign '=' between the two expressions that are equal to eachother. For instance, we use mathematical formulae to describe curves in a two-dimensional coordinate system. Each curve is described by its relation between the x- and y-coordinates. The intersection of two curves is defined by the (x,y)-coordinates that satisfy both curve-formulae. This results in two equations with two unknowns: x and y. Except for parallel lines, two straight lines always have one unique intersection point. If we want to find the intersection point, we could plot the two lines, but that takes quite some time and a lot of paper if the intersection point is "far away". A better way to find the intersection point is to solve the two equations.

Waypoint 7: N 51º 27.VUS, E 5º 29.UTU

Assignment: What decimal number of 2 digits is written on the small white plate on the pole near a tree? Multiply this number by 60 and add F. Denote the result by WXY.
Exercise: Calculate

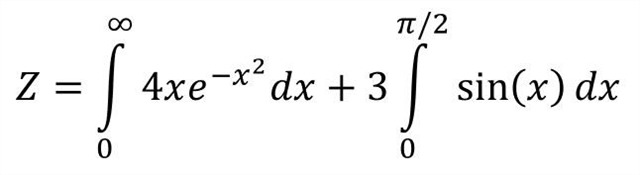
Sir Isaac Newton (1643 - 1727, England) Integral calculation was invented in the 17th century, in the same timeframe as differential calculation. Sir Isaac Newton was one of the inventors. Integral calculation belongs to a part of mathematics called analysis. Integrals are used to calculate "totals", like to total area under a curve, the total change of a metric if the change per unit of time is known, or the total mass of an object if the mass density is given for each point of the object. In its most elemetary, intuitive form, the integral of a function over the interval [a,b] equals the area between the curve and the horizontal coordinate axis, between the points and b. The integral over the interval [a,b] is denoted as; 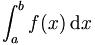The result is the area S under the curve. The integral of f(x) is the area between the curve y = f(x) and the x-axis in the interval [a,b].

Waypoint 8: N 51º 27.MYM, E 5º 29.ZWS

Assignment: Search for the cache!

You can check your final coordinate for this geocache on GeoChecker.com.