Ludolph van Ceulen
Holandský matematik Ludolph van Ceulen se narodil 28. ledna 1540 v Hildesheimu v Německu. Zřejmě neměl univerzitní vzdělání, protože jeho rodiče si nemohli dovolit mu je zaplatit.
Vyučoval šerm a matematiku v Delftu. V roce 1594 si otevřel šermířskou školu v Leidenu. V roce 1600 se dostal na technickou školu tamtéž. V posledních 10 letech svého života vyučoval na této škole aritmetiku a pevnost. Napsal řadu prací, z nichž jedna z nejdůležitějších byla O kružnici.

Van Ceulen je proslulý svým výpočtem p (pí), jednoho z nejstarších čísel (konstant) v matematice. Toto číslo určuje, kolikrát se průměr kružnice vejde do jejího obvodu. Van Ceulen spočítal toto číslo na 32 desetinných míst. Použil k tomu mnohoúhelník, který měl 262 stran. Strávil nad tím většinu svého života. Toto 32místné p má vyryto na svém náhrobku. Ten se nedochoval, v roce 2000 však byl obnoven. Číslo se po něm v Německu, u nás a v některých jiných zemích nazývá "Ludolfovo číslo". Spíše historické (ale např. v angličtině používané) je označení Archimédova konstanta po Archimédovi ze Syrakus.
Van Ceulen zemřel 31. prosince 1610 v nizozemském Leidenu.
Číslo π
π je matematická konstanta, která udává poměr obvodu jakéhokoli kruhu v eukleidovské rovině k jeho průměru; také je to hodnota poměru obsahu kruhu ke čtverci jeho poloměru. Její hodnota v desítkové soustavě je přibližně 3,14. Mnoho matematických, vědeckých a inženýrských rovnic obsahuje pí, což z něj dělá jednu z nejdůležitějších matematických konstant.
π je iracionální číslo, což znamená, že nemůže být vyjádřeno zlomkem m/n, kde m je celé číslo a n je přirozené číslo. To také znamená, že jej nelze vyjádřit konečným způsobem v desítkové soustavě, a to ani pomocí periody. Navíc je π dokonce transcendentní číslo, z čehož mimo jiné vyplývá, že ho nelze vyjádřit konečně dlouhou řadou algebraických operací s celými čísly; důkaz tohoto tvrzení byl výsledkem německé matematiky 19. století. V dějinách matematiky se objevují snahy o čím dál přesnější vyjádření π a pochopení jeho povahy; fascinace tímto číslem se promítla i mimo sféru matematiky.
Nejspíše pro jednoduchost své definice se π promítlo do populární kultury více než téměř všechny jiné matematické konstrukty. Stalo se nejspíše nejběžnějším společným tématem mezi matematiky a nematematiky. Zprávy o nejnovějším, nejpřesnějším odhadu π se běžně objevují v tisku. Nynější rekord v nejpřesnějším odhadu π v desítkové soustavě je 12 bilionů číslic. V aplikované matematice se většinou používá zaokrouhlení pouze na několik desítek desetinných míst. 11 desetinných míst π například stačí na odhad délky kružnice, která je velká jako Země, s chybou menší než jeden milimetr, a 39 desetinných míst stačí na jakoukoli představitelnou aplikaci.
Odhad čísla π
π se dá odhadnout narýsováním kružnice, změřením jejího průměru a její délky a následným vydělením délky průměrem. Další způsob, který navrhl Archimédés, je spočítat obvod on pravidelného mnohoúhelníku s n stranami s vepsanou kružnicí o průměru d. Potom lze vytvořit limitu posloupnosti, kde se n přibližuje nekonečnu
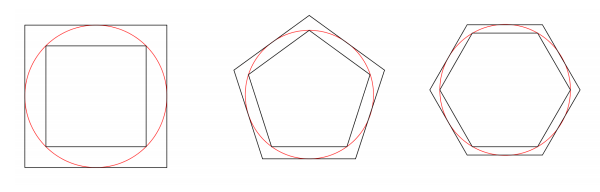
π lze také spočítat čistě matematickými metodami. Protože je transcendentní, nelze ho vyjádřit pomocí algebraické rovnice, v níž by se vyskytovaly jen racionální koeficienty. Vyjádření pomocí elementární aritmetiky často obsahuje řady, nebo sumační značení (např. „…“), což naznačuje, že vzorec je ve skutečnosti vzorcem pro nekonečnou řadu aproximací π. Čím více prvků sumace obsahuje, tím přesnější bude odhad.
Vzorce k vypočítání π mají požadované matematické vlastnosti, ale jsou těžko pochopitelné bez znalosti trigonometrie. Některé jsou ale jednodušší, například Leibnizova řada
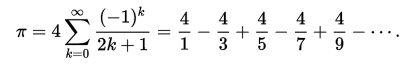
I když je tuto řadu jednoduché napsat a spočítat, nemusí být zpočátku jasné, proč je její výsledek π. Navíc je tak zdlouhavá, že je potřeba téměř 300 prvků, aby vyšla správně první dvě desetinná místa π.
Další metody jsou celkem složité, a jejich popis je mimo rozsah této keše. Tady je jejich výčet těch nejznámnějších:
- Taylorův a Maclaurinův rozvoj
- Gregoryho řada
- Machinův vzorec
- Newtonova metoda
- Eulerova metoda
- Ramanujanovy řady
Rekordy ve výpočtu π
| Rok vypočtení |
Kdo se o objev zasloužil |
Počet desetinných míst |
| 1400 |
Madhava ze Sangamagramy |
10 |
| 1424 |
Jamshīd al-Kāshī |
16 |
| 1596 |
Ludolph van Ceulen |
20 |
| 1615 |
Ludolph van Ceulen |
32 |
| 1621 |
Willebrord Snell |
35 |
| 1630 |
Christoph Grienberger |
38 |
| 1699 |
Abraham Sharp |
71 |
| 1706 |
John Machin |
100 |
| 1719 |
Thomas Fantet de Lagny |
112 |
| 1794 |
Jurij Vega |
137 |
| 1841 |
William Rutherford |
152 |
| 1844 |
Johann Martin Zacharias Dase |
200 |
| 1847 |
Thomas Clausen |
248 |
| 1853 |
Lehmann |
261 |
| 1855 |
Richter |
500 |
| 1874 |
William Shanks |
527 |
| 1946 |
D. F. Ferguson |
620 |
| 1947 |
D. F. Ferguson |
710 |
| 1947 |
D. F. Ferguson |
808 |
| 1949 |
D. F. Ferguson |
1 120 |
| 1949 |
John Wrench, L. R. Smith |
2 037 |
| 1954 |
S. C. Nicholson, J. Jeenel |
3 092 |
| 1957 |
G. E. Felton |
7 480 |
| 1958 |
Francois Genuys |
10 000 |
| 1958 |
G. E. Felton |
10 020 |
| 1959 |
Francois Genuys |
16 167 |
| 1961 |
Daniel Shanks, John Wrench |
100 265 |
| 1966 |
J. Guilloud, J. Filliatre |
250 000 |
| 1967 |
J. Guilloud, M. Dichampt |
500 000 |
| 1973 |
J. Guilloud, M. Bouyer |
1 001 250 |
| 1981 |
Kazunori Miyoshi, Yasumasa Kanada |
2 000 036 |
| 1981 |
Jean Guilloud |
2 000 050 |
| 1982 |
Yoshiaki Tamura |
2 097 144 |
| 1982 |
Yoshiaki Tamura, Yasumasa Kanada |
4 194 288 |
| 1982 |
Yoshiaki Tamura, Yasumasa Kanada |
8 338 576 |
| 1983 |
Y. Kanada, S. Yoshino, Y. Tamura |
16 777 206 |
| 1985 |
Bill Gosper |
17 526 200 |
| 1986 |
David. H. Bailey |
29 360 111 |
| 1986 |
Yasumasa Kanada, Yoshiaki Tamura |
33 554 414 |
| 1986 |
Yasumasa Kanada, Yoshiaki Tamura |
67 108 839 |
| 1987 |
Y. Kanada, Y. Tamura, Y. Kubo a kolektiv |
134 214 700 |
| 1988 |
Yasumasa Kanada, Yoshiaki Tamura |
201 326 551 |
| 1989 |
Gregory Chudnovsky, David Chudnovsky |
480 000 000 |
| 1989 |
Gregory Chudnovsky, David Chudnovsky |
535 339 270 |
| 1989 |
Yasumasa Kanada, Yoshiaki Tamura |
536 870 898 |
| 1989 |
Gregory Chudnovsky, David Chudnovsky |
1 011 196 691 |
| 1989 |
Yasumasa Kanada, Yoshiaki Tamura |
1 073 740 799 |
| 1991 |
Gregory Chudnovsky, David Chudnovsky |
2 260 000 000 |
| 1994 |
Gregory Chudnovsky, David Chudnovsky |
4 044 000 000 |
| 1995 |
Yasumasa Kanada, Daisuke Takahashi |
4 294 960 000 |
| 1995 |
Yasumasa Kanada, Daisuke Takahashi |
6 442 450 938 |
| 1997 |
Yasumasa Kanada, Daisuke Takahashi |
51 539 600 000 |
| 1999 |
Yasumasa Kanada, Daisuke Takahashi |
68 719 470 000 |
| 1999 |
Yasumasa Kanada, Daisuke Takahashi |
206 158 430 000 |
| 2002 |
Yasumasa Kanada a kolektiv |
1 241 100 000 000 |
| 2009 |
Daisuke Takahashi a kolektiv |
2 576 980 377 524 |
| 2009 |
Fabrice Bellard |
2 699 999 990 000 |
| 2010 |
Shigeru Kondo |
5 000 000 000 000 |
| 2011 |
Shigeru Kondo |
10 000 000 000 050 |
| 2013 |
Shigeru Kondo |
12 100 000 000 050 |
Keš nehledej na úvodních souřadnicích. Keš najdete na:
N XX° XX.XXX E YYY° YY.YYY
přičemž XXXXXXX => 5237430 a YYYYYYYY => 45725676

