#8 Matematica - Le frazioni Mystery Cache

La serie della matematica #8 - Le frazioni
Una piacevole passeggiata nel bosco dopo un compito di matematica.

Mathematics power trail #8 - The Fractions
Walking in the easy woods after the homework of math.  

Attenzione, il cache non si trova sulle coordinate del listing, per trovare le coordinate finali devi fare un po' di calcoli.

Parcheggia al parcheggio indicato e comincia dal primo cache. Dopo aver trovato l'ottavo cache potrai trovare le coordinate del bonus che si trova vicino la strada di ritorno al parcheggio. Tutti cache tranne il bonus sono posizionati poche decine di metri dal sentiero. La serie è composta da 8 cache più bonus. Sul logbook trovi le cifre importanti per poter trovare il bonus. Non dimenticare di segnarle.

Questo e' il cache numero 8 e questa volta ci divertiamo con le frazioni.

Le frazioni sono un sistema di rappresentare i numeri razionali. Ogni numero razionale può essere espresso come frazione. La frazione è composta da due numeri. Il primo, sopra la linea, si chiama numeratore, l'altro, sotto la linea, si chiama denominatore. Il valore della frazione e' uguale al risultato della divisione del numeratore per denominatore. Perché questi nomi strani? Perché il denominatore da il nome alla frazione e il numeratore dice quante parti abbiamo calcoliamo. Per esempio 3/4 = "tre quarti". In questo caso, il nome "quarto" dice che abbiamo diviso una torta a quattro parti, il "tre" dice che abbiamo preso tre di queste parti. La frazione dice che abbiamo 3/4 della torta. Quanto è? E' il 3 diviso 4, quindi 0.75.

Il vantaggio delle frazione è, che possiamo calcolare a massima precisione. Qualsiasi frazione può essere rappresentata come un numero decimale, però solo alcune frazioni danno un numero decimale preciso. Per esempio 1/4 convertito in un numero decimale da 0.25 preciso. Invece 1/22 da il risultato 0.045454454545454545454545454545454545454545... fino al infinito. La sequenza 45 si ripete infinite volte. Quindi il numero 1/22 è periodico - vuol dire che è composto da una sequenza dei numeri ripetuta infinite volte. Facendo calcoli con numeri periodici senza fare attenzione a questa particolarità, come per esempio calcolandoli con una calcolatrice, probabilmente non arriviamo al risultato preciso. Trovando invece la frazione corrispondente a questo numero periodico possiamo fare i calcoli nel modo assolutamente preciso. Attenzione però ai numeri irrazionali come per esempio il π, questi non possono essere convertiti alle frazioni.

Ma quante cifre decimali può avere un numero razionale n/m? Non potrebbe succedere che la sequenza non finisce mai? La risposta è più semplice di quanto potrebbe sembrare. Immaginiamo la divisione di n:m in collona. Dividiamo i due numeri a scriviamo la razione. Aggiungiamo il punto decimale, il resto moltiplichiamo per 10 e dividiamo con m. Dalla divisione esce la razione che rappresenta una cifra del risultato e un resto che è minore di m. Quindi il resto può avere solo m valori diversi diversi. Nel caso che resto è 0 abbiamo finito e il numero non è periodico. Altrimenti al massimo dopo m divisioni deve per forza arrivare lo stesso resto che abbiamo già avuto prima, quindi da qui la sequenza si ripeterà e avremo il numero periodico.

Con le frazioni possiamo fare tutte le operazioni matematiche fondamentali, come addizione, sottrazione, moltiplicazione, divisione e tante altre. Nel caso in cui dobbiamo risolvere le equazioni nel modo algebrico (quindi non con i numeri ma con i simboli), siamo praticamente obbligati a risolverle usando i calcoli delle frazioni. Infatti, anche per questo motivo, quando abbiamo una equazione che porta ad una divisione, quasi sempre la scriviamo come frazione. Per esempio v=s/t, non v=s:t.

Le operazioni fondamentali con le frazioni:

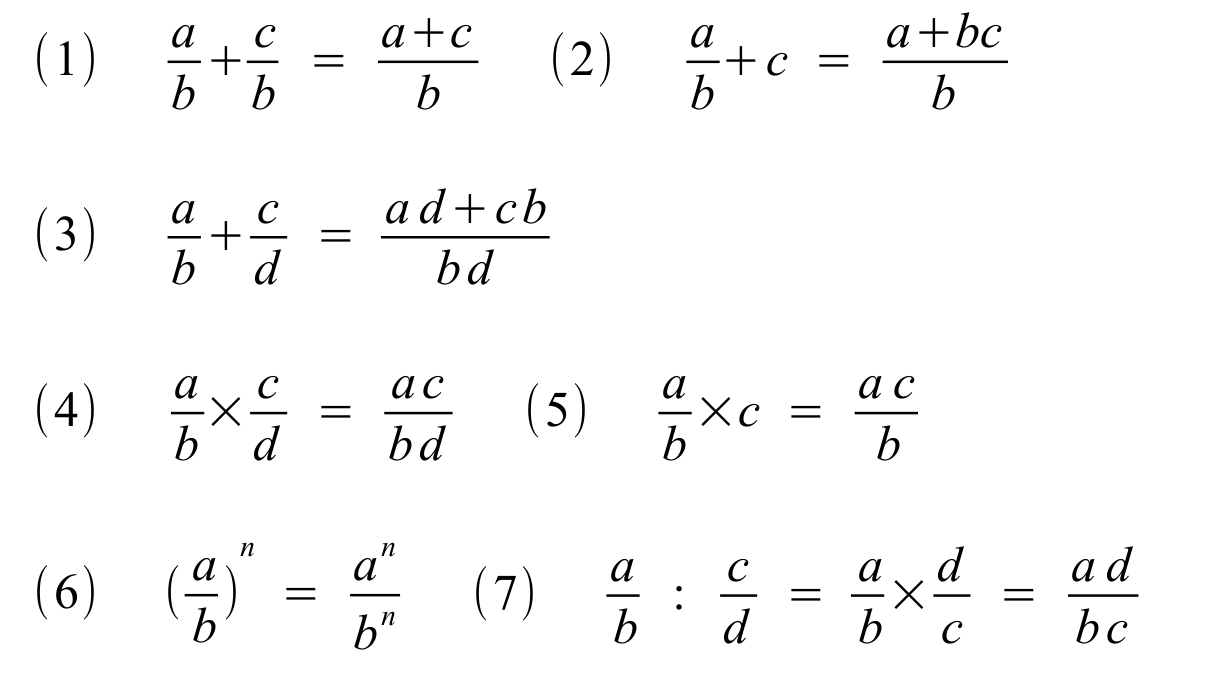
Una frazione può essere:

• riducibile - se il numeratore e il denominatore hanno un comune divisore maggiore di 1
• ridotta ai minimi termini – o irriducibile – se il numeratore e il denominatore sono numeri primi fra loro (cioè il loro GCD è 1)
• propria se il numeratore è minore del denominatore
• impropria se il numeratore è maggiore del denominatore
• apparente se il numeratore è multiplo del denominatore o uguale ad esso
• unitaria se ha numeratore 1
• decimale se il denominatore è una potenza di 10
• diadica se il denominatore è una potenza di due

Le frazioni riducibili possono essere semplificate. Per esempio 12/18 che ha il comune divisore 6. In tal caso la frazione si può semplificare dividendo sia il denominatore che il numeratore con il comune divisore. Nel nostro caso otteniamo la frazione 2/3 che è uguale al 12/18, ma è più semplice. Trovando il MCD (GCD) ovvero 'Massimo Comune Divisore' (Greatest Common Divisor) del numeratore e il denominatore e dividendo entrambi con questo divisore otteniamo sempre una frazione irriducibile.

Ma come si trova questo MCD/GCD? Lo so, che sto ripetendo sempre le stesse cose - usando la Calcolatrice wp34s, in particolare la sua funzione GCD. Comunque bisogna anche sapere come si fa. Se uno si trova una scusa tipo 'Ma a me a cosa serve di saper contare, tanto, abbiamo le calcolatrici', si deve rispondere con la domanda 'Chi le costruirà quando si romperà l'ultima?', Quindi dimentichiamo per un'attimo la funzione GCD sulla calcolatrice e andiamo a calcolarla manualmente. Non è una funzione triviale, si deve procedere per iterazioni. Vuol dire che dobbiamo ripetere lo stesso calcolo più volte fino a che non troviamo il risultato.

Il metodo l'ha inventato circa negli anni -400 il matematico greco Euclides. E' uno dei algoritmi più antichi usati finora. E' basato sul fatto che nel caso che a>b, GDC(a,b)=GDC(a-b,b). Sottraendo sempre il numero più basso dal numero più alto dobbiamo prima o poi arrivare ai numeri abbastanza piccoli da poter risolvere questo problema. Infatti, quando arriviamo alla situazione che entrambi numeri sono uguali, vuol dire che entrambi sono divisibili con sé stessi, quindi il risultato è uguale a questo valore. Per semplificare la condizione di fine calcolo possiamo dire che quando il valore della ultima sottrazione raggiunge zero, vuol dire che abbiamo sottratto due numeri uguali, quindi quelli erano il risultato.

Ora vediamo cosa succederebbe se il numero a fosse molto più grande del b. Il b è piccolo, quindi dobbiamo sottrarre a=a-b. Ma a era molto grande, quindi dobbiamo di nuovo sottrarre a=a-b. E così via finché non arriviamo al a<b. Ma perché fare tanta fatica. La stessa cosa fa l'operazione modulo, ovvero resto dopo la divisione. Quindi possiamo modificare il nostro algoritmo al GCD(a,b)=GCD(a mod b,b).

Allora ora vediamo come calcolare il GCD(a,b):

1. sulla prima riga scrivi il piu' grande dei due numeri
2. sulla seconda riga scrivi il piu' piccolo dei due numeri
3. sulla prossima riga scrivi il resto dopo la divisione della penultima riga con ultima riga
4. se il numero che hai scritto era maggiore di 0, continua sul punto 3
5. altrimenti il numero sulla penultima riga è il risultato.

Non è poi così complicato, vero? E funziona da quasi 2500 anni.

Sulla calcolatrice wp34s si potrebbe calcolare in questo modo. Sullo stack metti le due cifre e poi per ogni passo fai:
[h] [RMDR] [RCL] [L] [x↔y]
Comunque non dimenticare che hai sempre a disposizione direttamente la funzione GCD

Torniamo però alle frazioni. Come possiamo trasformare un numero decimale alla frazione?

Per i numeri non periodici è semplice. Risulta proprio dalla definizione del numero decimale. Semplicemente dobbiamo fare una frazione decimale, cioè frazione con denominatore uguale a 10ⁿ dove n è il numero di cifre dopo il punto decimale e il numeratore uguale al numero senza il punto decimale. Quindi, per esempio 1.2345 = 12345/10⁴ = 12345/10000. Questo risultato possiamo ancora semplificare. GCD(12345,10000)=5, quindi dividiamo sia il numeratore che il denominatore con il numero 5, quindi il risultato finale è 2469/2000.

Come fare però per i numeri periodici? Qui la situazione è un pò più complicata, ma sempre sorprendentemente semplice. Prima vediamo un fatto interessante. Il numero 0.99 periodico è uguale a 1. Ma come è possibile? Perché 0.99 periodico diviso 3 è senza dubbio 0,33 periodico, il che è esattamente 1/3. E visto che 3 per 1/3 è 1, vuol dire che 0.99 periodico è 1. Ora proviamo dividere 0.999999 periodico con 999. Avremo 0,001001001001 periodico. Moltiplicando un numero così con qualsiasi numero a tre cifre abc avremo un numero 0.abcabcabc, quindi 0.abc periodico. Questo ovviamente funziona anche con qualsiasi altro numero di cifre, quindi se abbiamo un numero periodico che ha per esempio due cifre periodiche, moltiplicheremo 1/99 per le due cifre periodiche.

Così possiamo trasformare qualsiasi numero puramente periodico alla frazione. Ma cosa fare per i numeri che hanno una parte non periodica e altra periodica, come per esempio 1.23789789789789 Semplicemente dividiamo il numero a due parti - periodica e non periodica, quindi nel nostro caso 1.23+0.789789789789/100, quindi farà 123/100+789/999/100. Facendo un pò di calcoli con le frazioni e tenendo conto che 999=1000-1 possiamo semplificare il calcolo a:

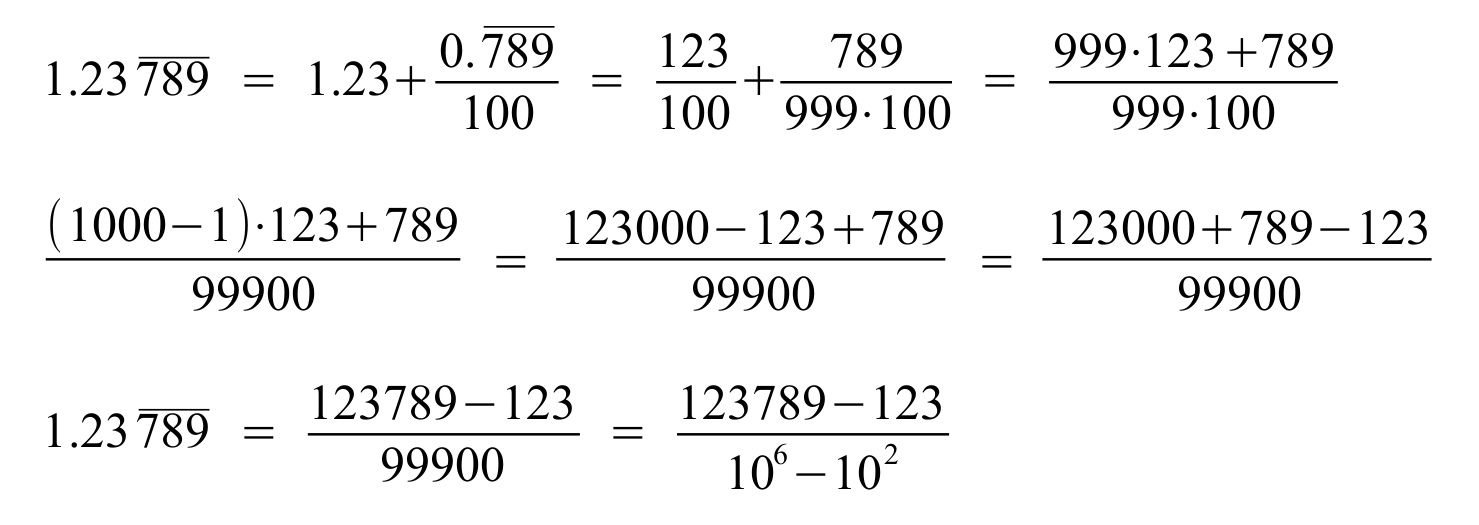
Quindi come vediamo, per trasformare un numero periodico alla frazione prendiamo tutte le cifre del numero meno le cifre non periodiche diviso con un numero composto da tanti 9 quante sono le cifre periodiche e tanti zeri quante sono le cifre non periodiche dopo il punto decimale. Oppure come sulla ultima equazione, facciamo la divisione con 10^d+1 - 10ⁿ dove d è il numero di tutte le cifre decimali ed n è il numero delle cifre non periodiche dopo il punto decimale.

Ora sappiamo tutto che bisogna sapere, quindi ora possiamo cercare le coordinate finali. Il cache si trova sulle coordinate:
N 45° 03.ABC   E 007° 27.DEF
dove
ABC è il denominatore della frazione irriducibile equivalente a 99221/210023
DEF è il numeratore della frazione irriducibile equivalente a 12.6136 di qui 36 è periodico

Arrivando dal #7 non dimenticare di visitare il masso erratico

Attention, the cache is not placed at the coordinates of listing. You must calculate the final coordinates.

Leave the car at the parking place, see the waypoint and begin with the first cache of the series. After you have found the last cache you can found the bonus cache located near the path for the parking. There are 8 caches plus bonus. Note the code on logbook that you need for search the bonus. All caches expect the bonus are placed few meters from the path.

to be translated...

the cache is here: