DEBB - Festigkeitslehre Mystery Cache

Ein weiteres Buch aus Meiningens ExBLOWdierter Bibliothek ist gelandet...

Die Festigkeitslehre als Teilgebiet der Technischen Mechanik beschäftigt sich mit der Widerstandsfähigkeit von Körpern unter Belastung und soll Spannungen und Verformungen in Körper bzw. Bauteilen ermitteln sowie den Nachweis erbringen, dass ein Versagen des Bauteils mit ausreichender Sicherheit ausgeschlossen werden kann. Unter Versagen des Bauteils versteht man u. a. das Auftreten zu großer Spannungen und/oder Verformungen.

Nachfolgend soll anhand eines Beispiels die Berechnung der Verformung eines Körpers veranschaulicht werden. Wer sich mit dem Thema auskennt, kann diesen Teil natürlich überspringen und sich gleich der Aufgabe am Ende zuwenden. Bei dem angeführten Beispiel handelt es sich um einen einfachen Balken auf einem Fest- sowie einem Loslager, der durch eine konstante Streckenlast belastet wird. Dieser Fall wäre z.B. eine vereinfachte Darstellung einer Brücke, die nur durch ihr Eigengewicht belastet wird. Solche Objekte sollten jedem Cacher bekannt sein. Die meisten sind ja schon einmal darübergelaufen und einige hingen auch schon darunter.

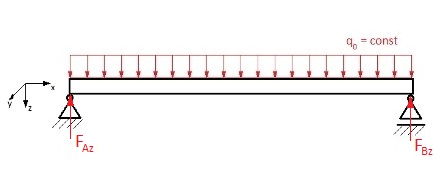
Die vereinfachte Darstellung sieht in etwa aus wie folgt

Zunächst sind die Auflagereaktionen, also die Kräfte in den Lagern zu bestimmen. Der Vollständigkeit halber gehe ich bei der Bestimmung der Lagerreaktionen noch ein wenig ins Detail.
Sowohl Fest- als auch Loslager können nur Kräfte, jedoch keine Momente aufnehmen. Das Loslager (Lager B) kann im Gegensatz zum Festlager (A) nur Kräfte in z-Richtung, aber nicht in x-Richtung aufnehmen.
Im Bild ist ein Koordinatensystem dargestellt. Die Vorzeichen der Kräfte und Momente ergeben sich aus der Richtung der Koordinatenachsen. Bspw. haben Kräfte, die senkrecht von oben nach unten wirken, ein positives Vorzeichen (z-Achse zeigt nach unten). Momente zeigen in Richtung der y-Achse. Das Vorzeichen wird dabei durch die „rechte-Faust-Regel“ ermittelt. „Dreht“ ein Moment bspw. im Uhrzeigersinn, hat es ein negatives Vorzeichen (y-Achse zeigt „aus der Zeichenebene heraus“). Der Koordinatenursprung (x = 0) liegt am Lager A.

Zurück zum Beispiel. Da die Streckenlast q₀ nur in senkrechter Richtung (z-Richtung) wirkt, müssen auch nur die Reaktionskräfte in z-Richtung betrachtet werden. Die Vorzeichen der Kräfte sind wie eben beschrieben zu wählen. Wenn sich das Vorzeichen bei der späteren Berechnung umkehrt, ist das kein Fehler. Es bedeutet lediglich, dass die Kraft entgegengesetzt zur angenommenen Richtung wirkt. Die Summe der Kräfte muss in jedem Fall 0 sein (actio = reactio)! Die Kräfte in z-Richtung ergeben sich wie folgt

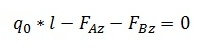(Anm.: Die Belastung durch eine Streckenlast q₀ [in N/m] ist abhängig von der Länge l des Körpers. Die resultierende Kraft beträgt F_res = q₀ * l)
Wie man sieht, enthält die Gleichung bei bekanntem q₀ zwei Unbekannte, kann also nicht gelöst werden. Zur Bestimmung der Unbekannten müssen noch die Momente (y-Richtung) betrachtet werden. Als „Drehpunkt“ wird das Lager B festgelegt. Das Moment der Kraft F_Az bezogen auf den Drehpunkt B beträgt M_Az = - F_Az * l (das negative Vorzeichen resultiert aus der Drehrichtung im Uhrzeigersinn).
Zur Bestimmung des Moments durch die Streckenlast q₀ kann die Streckenlast durch eine äquivalente Einzellast F_q0 = q₀ * l mit Angriffspunkt in der Mitte der Streckenlast (x = l/2) ersetzt werden. Das Moment beträgt somit M_q0 = q₀ * l * l/2 = q₀ * l²/2. Das Moment der Kraft F_Bz ist 0, da sie durch den Drehpunkt verläuft. Wie zuvor erwähnt können weder Fest- noch Loslager Momente aufnehmen, d.h. ein Einspann- bzw. Lagermoment kommt in der Gleichung nicht vor. Es gilt das Momentengleichgewicht

Durch Umstellen nach F_Az und Einsetzen in die erste Gleichung ergibt sich

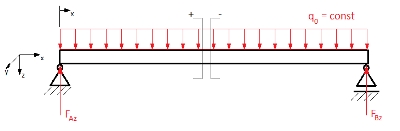
Die Kräfte F_Az und F_Bz sind also betrags- und richtungsmäßig gleich. Nachdem nun die Lagerreaktionen bekannt sind, können die Schnittgrößen (Querkraft F_Q und Biegemoment M_b) ermittelt werden. Diese sind nötig zur Bestimmung der Verformung. Das "Freischneiden" des Trägers wird im folgenden Bild durch die eckigen Klammern ][ dargestellt. Die linke Seite ist das positive, die rechte das negative Schnittufer.

Bei der Bestimmung der Schnittgrößen sind die sog. Stetigkeitsbereiche zu berücksichtigen. Die Unterteilung des Körpers in Stetigkeitsbereiche ergibt sich durch Lagerungen, freie Enden des Körpers, Einzellasten, Anfang und Ende von Streckenlasten, Änderungen des Querschnitts und Knicke. Die Betrachtung der Schnittgrößen muss für jeden Stetigkeitsbereich separat erfolgen. Im Beispiel existiert nur ein Stetigkeitsbereich. Zur Bestimmung der Schnittgrößen wird der Träger im jeweiligen Stetigkeitsbereich freigeschnitten. Es werden jeweils nur die Kräfte und Momente auf der Seite des gewählten Schnittufers betrachtet.

Im Bild ist der Trägerbereich am positiven Schnittufer dargestellt. Die Wahl des Schnittuffers ist für die Berechnung der Schnittgrößen aber prinzipiell egal. Die Schnittgrößen F_Q und M_b halten den geschnittenen Träger im Gleichgewicht. Beide Größen werden wegen des positiven Schnittufers auch mit positivem Vorzeichen angenommen. Auch hier gilt: Dreht sich das Vorzeichen durch die Berechnung um, wirkt die Kraft / das Moment lediglich entgegen der angenommenen Richtung.
Die Querkraft F_Q resultiert aus allen Kräften, die quer zur Schnittfläche wirken, im Beispiel also aus allen Kräften in z-Richtung. Es gilt wieder das Kräftegleichgewicht.

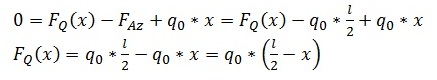Die Kraft F_Bz liegt auf der anderen Seite des Freischnittes und muss nicht berücksichtig werden. Bei der Streckenlast muss nur der Bereich berücksichtigt werden, der sich auf der Seite des positiven Schnittufers befindet, d.h. der Teil der Streckenlast über der Strecke x. Hier wird bereits deutlich, dass die Querkraft keines Falls konstant ist, da die aus der Streckenlast resultierende Kraft von x abhängig.
Das Biegemoment im Querschnitt an der Stelle x wird durch Betrachtung der durch die Kräfte und Lasten auftretenden Momente ermittelt. Zur Bestimmung des Momentes aus der Streckenlast wird wieder die äquivalente Vergleichskraft herangezogen. Sie beträgt q₀ * x und greift in der Mitte der betrachteten Strecke x (also an der Stelle x/2) an.

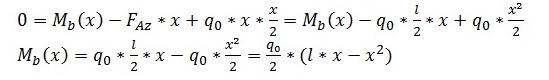Damit kann nun die Verformung des Körpers berechnet werden. Hierzu muss zunächst die Differentialgleichung (kurz DGL) der Biegelinie aufgestellt werden. Diese lautet in der allgemeinen Form w‘‘(x) = -M_b/E*I, wobei E der Elastizitätsmodul und I das Flächenträgheitsmoment ist. E ist abhängig von Material des betrachteten Körpers, I von dessen Querschnitt.
Die erste Integration w‘(x) der DGL gibt den Biegewinkel (bzw. den Tangens des Biegewinkels - bei ausreichend kleinem Winkel ist der Tangens annähernd gleich dem Winkel) an der Stelle x an, die zweite Integration w(x) die Durchbiegung. Setzt man die zuvor aufgestellte Gleichung für M_b in die DGL und führt die Integration durch, so erhält man

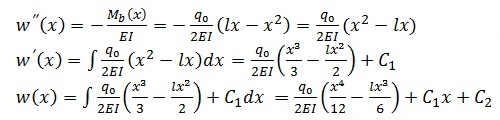Die Bestimmung der Integrationskonstanten C₁ und C₂ erfolgt aus den Randbedingungen des Lastfalls. Diese sind durch Überlegung zu Ermitteln bzw. einer Formelsammlung zu entnehmen. Im Beispiel gilt, dass die Durchbiegung w an den beiden Lagern 0 ist; es gilt also w(x=0) = 0 und w(x=l) = 0. Aus den Randbedingungen folgt

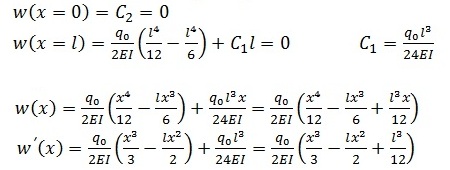Die maximale Durchbiegung tritt im Beispiel in der Mitte des Trägers, also an der Stelle x = l/2 auf. Sie beträgt somit w_max = 5q₀l⁴/384EI.

Um noch die Vorgehensweise bei zusammengesetzten Belastungen sowie mehreren Stetigkeitsbereich zu zeigen, erweitere ich das Beispiel um eine Einzellast, die an der Stelle a zwischen den beiden Lagern angreift. Das könnte bspw. ein besonders dicker Cacher sein, der auf der Brücke steht. Wegen der einfacheren Rechnung lege ich mal fest, dass a = l/2 ist, der Cacher also in der Mitte der Brücke steht. Bei zusammengesetzten Lastfällen gilt das sog. Superpositionsprinzip (Superposition = Überlagerung), d.h. der zusammengesetzte Lastfall wird so zerlegt, dass mehrere einfache (und auch einfach zu rechnende) Lastfälle entstehen. Für das Beispiel bedeutet das, dass man neben dem bereits betrachteten Fall der Belastung durch eine Streckenlast nur noch den Fall der Einzellast berechnen muss und die Werte für Querkraft, Biegemoment, Biegewinkel und Durchbiegung im Anschluss einfach addiert.

Im Folgenden wird nur noch der Fall „Einzellast“ betrachtet. Zunächst werden wieder die Lagerreaktionen bestimmt. Ich verwende wieder dieselben Bezeichnungen der Kräfte und Momente wie bei der Streckenlast. Das Kräftegleichgewicht in z-Richtung lautet

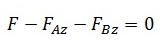Es sind wieder zwei Unbekannte vorhanden, also muss auch hier das Momentengleichgewicht herangezogen werden. „Drehpunkt“ sei wieder Lager B. Das Moment der Kraft F ist somit M_F = F * l/2. Das Moment von F_Az ist wie im ersten Beispiel M_Az = - F_Az * l. Durch Aufstellen des Momentengleichgewichts, Umstellen und Einsetzen in die Gleichung des Kräftegleichgewichts erhält man

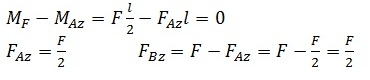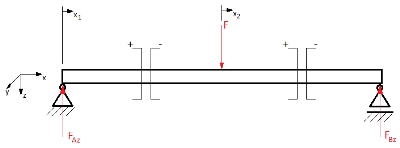
Als nächstes folgt die Bestimmung der Schnittgrößen. Die Einzellast F teilt den Träger in zwei Stetigkeitsbereiche x₁ und x₂. Die Schnittgrößen müssen für jeden Stetigkeitsbereich einzeln bestimmt werden.

Zunächst werden F_Q und M_b für den Bereich x₁ mit 0 ≤ x₁ ≤ a bzw. 0 ≤ x₁ ≤ l/2 ermittelt. Ich wähle das positive Schnittufer.

Es gilt für F_Q und M_b

Die DGL der Biegelinie sowie ihre erste und zweite Integration ergeben sich wie folgt

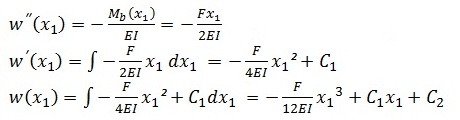Zur Bestimmung der Integrationskonstante C₂ wird wieder die Randbedingung herangezogen. Aus w(x₁=0) = 0 folgt C₂ = 0.
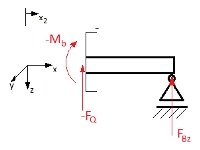
Um C₁ bestimmen zu können, muss zunächst der Stetigkeitsbereich x₂ mit 0 ≤ x₂ ≤ b bzw. 0 ≤ x₂ ≤ l/2 betrachtet werden. Ich beziehe mich diesmal auf das negative Schnittufer. Mit dem positiven ginge es aber genauso.

Die Schnittgrößen –F_Q (negativ weil negatives Schnittufer) und –M_b werden ermittelt. Bei der Berechnung von –M_b ist zu beachten, dass der Abstand der Kraft F_Bz zum entsprechenden Querschnitt mit zunehmendem x₂ kleiner wird.

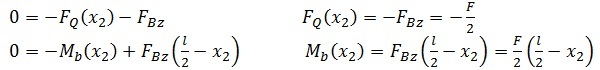Durch Aufstellen der DGL erhält man

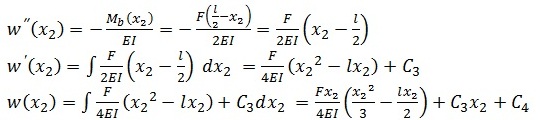Neben der Randbedingung w(x₂=b) = 0 gelten außerdem die Übergangsbedingungen w(x₁=a) = w(x₂=0) und w‘(x₁=a) = w‘(x₂=0). Diese Bedingungen gelten, weil die Biegelinie keinen Sprung und keinen Knick haben darf. An dieser Stelle kürze ich das Ganze mal ab. Die paar Werte in die Gleichungen einsetzen und nach den gesuchten Größen umstellen kann ja jeder. Man erhält

Die Gleichungen für w‘(x₁), w(x₁), w‘(x₂) und w(x₂) lauten dann

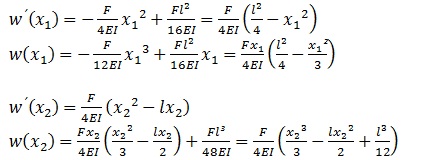Die maximale Durchbiegung tritt wieder in der Mitte des Trägers auf, also an der Stelle x₁ = l/2 bzw. x₂ = 0. Sie beträgt w_max = Fl³/48EI.
Wie zuvor erwähnt können nun die Werte der beiden einzelnen Lastfälle addiert werden, um die Werte des zusammengesetzten Lastfalls zu erhalten. Diesen Schritt spare ich mir aber. Mit bekannten Werten von l, q₀, F, E und I kann also die maximale Durchbiegung der (idealisierten) Brücke aus dem Beispiel berechnet werden.

Soviel zur Einführung in die Thematik. Ich hoffe, ich konnte einen Einblick in die Vorgehensweise verschaffen. Und um euer neu erworbenes Wissen gleich mal auf die Probe zu stellen, folgt nun eine kleine theoretische Übung mit anschließendem Praxisteil.

Theorieteil:
Gegeben sei ein Baum, ein weiteres den meisten Cachern bekanntes Objekt. An diesem Baum befindet sich in beliebiger Höhe ein zum Boden paralleler Ast der Länge l mit rundem konstantem Querschnitt mit Durchmesser d – der Ast kann also als ein Zylinder betrachtet werden. An diesem Ast hängt ein Seil im Abstand a vom Stamm. Um die Kräfteverhältnisse nicht unnötig kompliziert zu machen, postuliere ich (so was wollte ich schon immer mal schreiben), dass das Seil am Ast festgeknotet ist und keine Eigenmasse hat. Am Seil hängt ein Cacher. Der Masseschwerpunkt des Cachers liegt auf einer Achse mit dem Seil.

Gegeben sind weiterhin folgende Größen:
Dichte von Holz ρ_Holz = 649kg/m³
Länge des Astes l = 1500mm
Abstand a = 1008mm
Durchmesser des Astes d_Ast = 100mm
Volumen des Cachers V_Cacher = 0,075m³
Dichte des Cachers ρ_Cacher = 1088kg/m³
Elastizitätsmodul von Holz E_Holz = 13001N/mm²

Das Flächenträgheitsmoment des Astes I_Ast [in mm⁴] ist selbst zu bestimmen.

Die Verbindung von Ast und Stamm kann als feste Einspannung angesehen werden. Es handelt sich im Beispiel also um einen Kragarm, der durch eine konstante Streckenlast (Eigengewicht des Astes) und eine Einzellast (Masse des Cachers) belastet wird.

Gesucht sind die folgenden Werte:
Durchbiegung des Astes an der Stelle, an der das Seil befestigt ist – w(x = a) [in mm]
Biegewinkel (bzw. Tangens vom Biegewinkel) des Astes am freien Ende – w‘(x = l)

Rechnet durchweg mind. auf 3 Nachkommastellen genau.

Jetzt könnte natürlich die Frage auftauchen, wozu das Ganze? Ist eigentlich ganz klar: Wir können sagen, um wieviel sich der Ast uns entgegen neigt, wenn wir mal wieder mit dem Seil auf einen Baum klettern. Ist doch gut zu wissen, oder? Ihr könnt ja beim nächsten Klettercachen mal nachmessen. Außerdem könnt ihr, wenn ihr die Eckdaten des Baumes kennt und entsprechende Vergleichswerte für zulässige Durchbiegung und Spannung etc. habt, vorher mal überschlagen, ob der Ast euer Gewicht überhaupt trägt. Wär ja schlimm, wenn man fast oben ist und der Ast bricht plötzlich ab!
In der Praxis werden die Werte allerdings etwas anders ausfallen. Meist wird das Seil ja über den Ast geworfen, was zur Folge hat, dass, je nach Neigungswinkel des am Boden fixierten Seilstranges, die Kraft, die an der Seilauflage auf den Ast wirkt, um bis zu Faktor 2 größer ist als die Gewichtskraft des Cachers (vgl. Flaschenzug). Außerdem ist die Astgeometrie meist auch etwas komplexer. Aber das steht in einem anderen Buch...

Praxisteil:
Begebt euch zu den Koordinaten

N 50° [ 33.001 + |w'(x=l)| ]
E 10° [ 15.842 + |w(x=a)| ]

und bergt den Cache analog dem Theorieteil! Ob ihr richtig gerechnet habt, könnt ihr von Prof. Dr. G. Otschegger kontrollieren lassen. Ihr braucht natürlich weder euer Seil an den Ast knoten, noch einen Meter vom Stamm weg klettern. Ich fand's nur schön für die Rechnung. Bringt bitte unbedingt einen Schraubendreher für Schlitzschrauben mit! Unterhalb der Dose habe ich noch eine Filmdose befestigt, die ihr als Ablage für die Schrauben nutzen könnt. Nicht dass die noch runterfallen.

Viel Spaß beim Rechnen! Ich freu mich schon auf rauchende Köpfe!

Noch eine Anmerkung zur difficulty. Ein D5 hab ich mir erstmal verkniffen. Die Rechnung ist durchweg logisch und eindeutig durchführbar und auch vom Umfang her überschaubar (Meine Lösung passt auf ein A4-Blatt, beidseitig beschrieben). Es muss nichts erraten oder probiert werden.
So eine Wertung ist natürlich immer subjektiv. Der gemeine Ingenieur (ob richtiger oder nicht sei mal dahingestellt) schüttelt sich die Rechnung mal eben aus dem Ärmel. Alle anderen haben ja im listing die Vorgehensweise beschrieben und finden mit Sicherheit auch im Netz genügend Material, getreu dem Motto: "Man muss nicht wissen wie's geht, sondern nur wo's steht.