Serie Algoritmy

Tato serie ma za cil seznamit Vas s jednoduchymi algoritmy, ktere treba bezne pouzivate (nebo vyuzivate) a mozna o tom ani nevite. V nekolika dilech (+ bonusovka po kazdych ctyrech - na bonusovku nebudete potrebovat sbirat zadna cisla z vicek ani nic podobneho) se mimo jine dozvite, jak Vase GPS vyhledava nejkratsi trasu po silnicich, jak se elektrifikovala Morava, nebo treba jak projit tunel, kdyz dochazi baterky. Pokud Vas tohle vsechno zajima, pak je tahle serie urcena prave Vam!

V tomto dile se seznamime s grafy a stromy.

Na zacatek nekolik definic:

V listingu budu pouzivat nekolik odbornych terminu, jejichz pochopeni je klicove pro pochopeni samotnych uloh. Proto venujte aspon minimalni pozornost nasledujicim definicim.

1. GRAF
   ... je usporadana dvojice mnoziny vrcholu V a mnoziny hran, spojujicich tyto vrcholy E. Pozor, neplette si tento pojem s pojmem grafu funkce! "N" znacime pocet vrcholu, "M" pocet hran.
2. KRUZNICE
   Pro dva ruzne vrcholy v1 a v2 na kruznici plati, ze z v1 do v2 lze po hranach dojit dvema ruznymi zpusoby.
3. STROM
   ... je graf, ktery neobsahuje kruznici. Tj. z kazdeho vrcholu do kazdeho jineho vrcholu se lze (po hranach) dostat jen jednim zpusobem.
4. KOSTRA GRAFU
   ... byva definovana jako maximalni podstrom grafu. Tzn. strom, ktery spojuje vsechny vrcholy grafu nekterymi hranami z mnoziny E. Graf ma obvykle vetsi mnozstvi ruznych koster, vsechny ale maji N-1 hran pri N vrcholech (dukaz snadny).
5. MINIMALNI KOSTRA
   V ohodnocenem grafu (kazda hrana ma navic prirazenu ciselnou hodnotu - VAHU) lze zadefinovat min. kostru grafu. Je to kostra, ktera ma nejmensi soucet vah pouzitych hran.
6. KOMPONENTA SOUVISLOSTI
   ... je takovy podgraf, ze ze vsech jeho vrcholu se po hranach da "dojit" do vsech ostatnich vrcholu tohoto podgrafu, ale do zadnych jinych.

Prevzato (a zlidsteno) z knizky "Kapitoly z diskretni matematiky".

Hledani minimalni kostry:

Na problem minimalni kostry grafu narazil jako jeden z prvnich Otakar Boruvka, kdyz v roce 1926 resil problem, jak co nejlevneji elektrifikovat Moravu (to je krasny priklad hledani minimalni kostry: vesnice jsou vrcholy a jejich pomyslne spojnice jsou hrany, ohodnocene porizovaci cenou el. vedeni).
My si zde predstavime 3 algoritmy: Kruskaluv, Boruvkuv a Jarnikuv.

Algoritmy si predvedeme na nasledujicim ohodnocenem grafu:

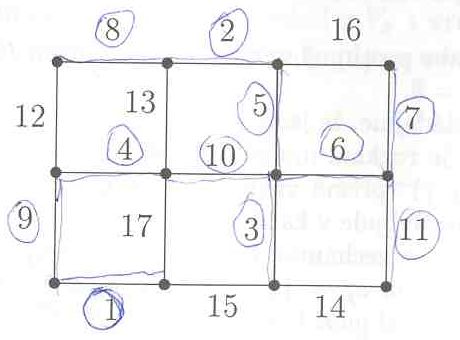
Z toho, ze si tam uz nekdo, kdo mel knizku pujcenou prede mnou, kreslil kostru, si nic nedelejte...

Kruskaluv algoritmus

... je nejjednodussi na implementaci a na dokazani, neni z nich ale nejrychlejsi. Take byva oznacovan jako "Hladovy". Princip je velice jednoduchy:

1. Z mnoziny hran si sestavime seznam setrideny podle vahy hran
2. Dokud nepridame N-1 hran do kostry:
 a. Vezmeme nejlevnejsi dosud nepridanou hranu a zkusime ji pridat
 b. Pokud vytvari s ostatnimi hranami kostry kruznici, opet ji odebereme
3. Kostra, kterou jsme postavili, je minimalni

Algoritmus si tu dokazovat nebudeme, snad jenom poukazu na jeho jednoduchost (zvlast pokud jde o to jej naprogramovat). Rozhodne jde ale o algoritmus nejpomalejsi (z nasich tri).

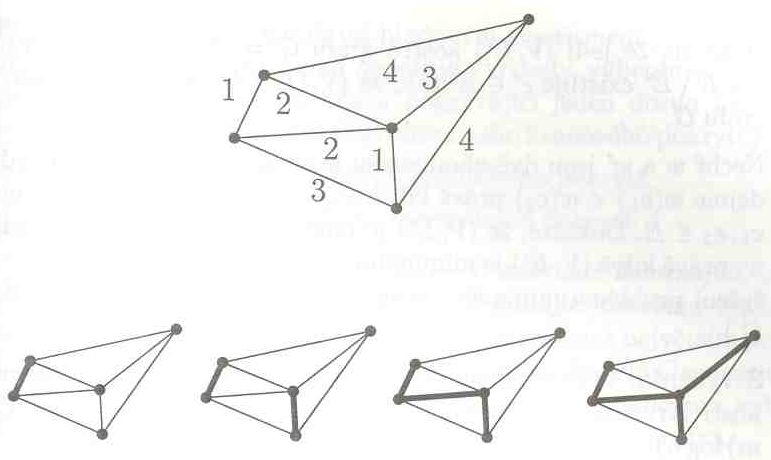
Jarnikuv algoritmus

Vojtech Jarnik, legendarni autor legendarnich spisu o diferencialnim a integralnim poctu, jeden z nejvetsich ceskych matematiku ma na svedomi i jeden z algoritmu na hledani minimalni kostry grafu. Objevil jej roku 1930, presto je tento algoritmus ve svete znam spis jako Primuv alg. podle Roberta C. Prima, ktery jej "objevil" roku 1957.
Muzete si vsimnout, ze algoritmus uz neni tak jednoduchy jako Kruskaluv:

1.  Vybereme si vrchol, ze ktereho budeme kostru stavet
// Muze to byt libovolny vrchol - v kostre nakonec musi byt vsechny.
2.  Najdeme nejlevnejsi hranu, ktera z nej vede a pridame ji do kostry.
// Tim mame jednu komponentu souvislosti, ktera obsahuje 2 vrcholy a N-1 komponent s jedim vrcholem.
  // Komponente, ktera je vlastne zakladem kostry, budeme rikat K.
3.  Dokud jde pridat hrana:
a.  Najdeme nejlevnejsi hranu, ktera vede z komp. K do jine komponenty a pridame ji do kostry.
4.  Mame minimalni kostru.

Casova slozitost tohoto algoritmu je mensi nez u Kruskala, ale programator za to zaplati slozitejsim programovanim.

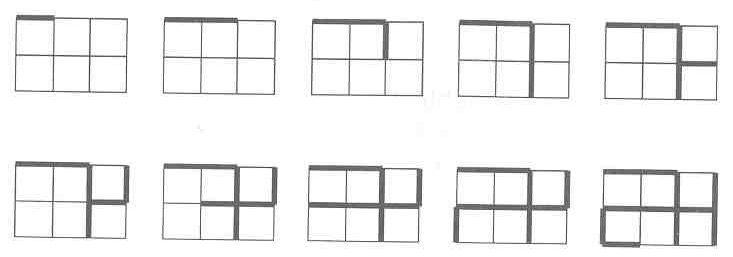
Boruvkuv algoritmus

Jak jiz bylo receno, pomoci tohoto algoritmu se elektrifikovala Morava. Na implementaci je asi nejslozitejsi, ale asymptotickou slozitost ma nejlepsi. Tady mame jeho modifikaci (v originale predpoklada, ze ruzne hrany maji ruzne vahy):

1.  Na zacatku je kazdy vrchol komponenta souvislosti.
2.  Dokud lze vykonat nasledujici krok:
   a.  Vezmeme postupne kazdou komponentu souvislosti:
      i.  Najdeme nejlevnejsi hranu, ktera vede do jine komponenty a obe komp. spojime.
3.  Mame minimalni kostru.

Jak vidite, je to jako pustit na graf nekolik (N) Jarniku najednou.

Finalka

No a ted by Vas nejspis zajimalo, kam jsem mohl zasit tu krabicku, co? Nebude zas tak jednoduche ji najit. Pokud nejste mistni, zahajte odlov na vychozich souradnicich - doveze Vas tam autobus 139 nebo 253. Nejezdete tam autem - NENI tam kde zaparkovat!
Do logu mi napiste, s pomoci jakeho algoritmu jste kesku hledali.
Tak a ted k souradnicim:
keska je v docela malebnem udolicku, odkud ani neni videt vetsina panelaku, na souradnicich N 49 ((A + 1)*934 - 10)/1000 E 014 ((A + 1)*391 + 29)/1000, kde A je celkova vaha minimalni kostry nasledujiciho grafu (napoveda: A je delitelne tremi):

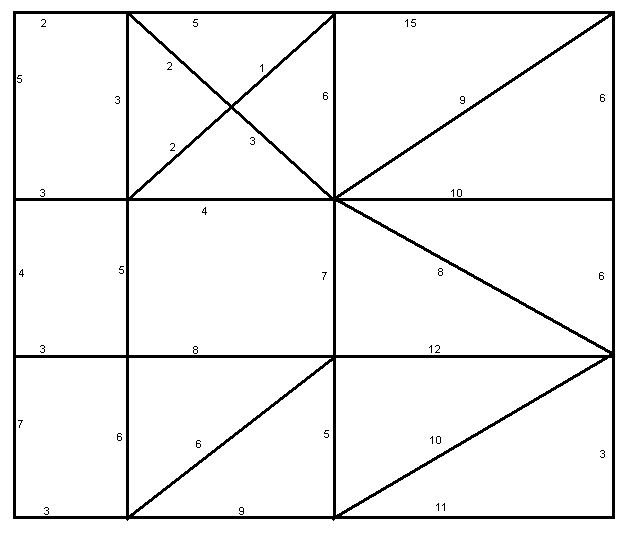
Provazej Vas Signal!

Zdroje:

• Kapitoly z diskretni matematiky
• internet